Max Blog

transformer整体结构分析总结

1 背景

之前的序列模型存在两个问题：

• t时刻的的计算依赖于$t-1$时刻的计算结果，模型无法并行计算
• 当序列较长的时候，LSTM等网络无法解决长距离依赖的问题

针对以上问题，transformer引入了Attention机制，解决了以上问题。

后续的表现也足以证明这个模型效果非常优秀。

2 模型结构

模型整体是一个encoder-decoder结构。

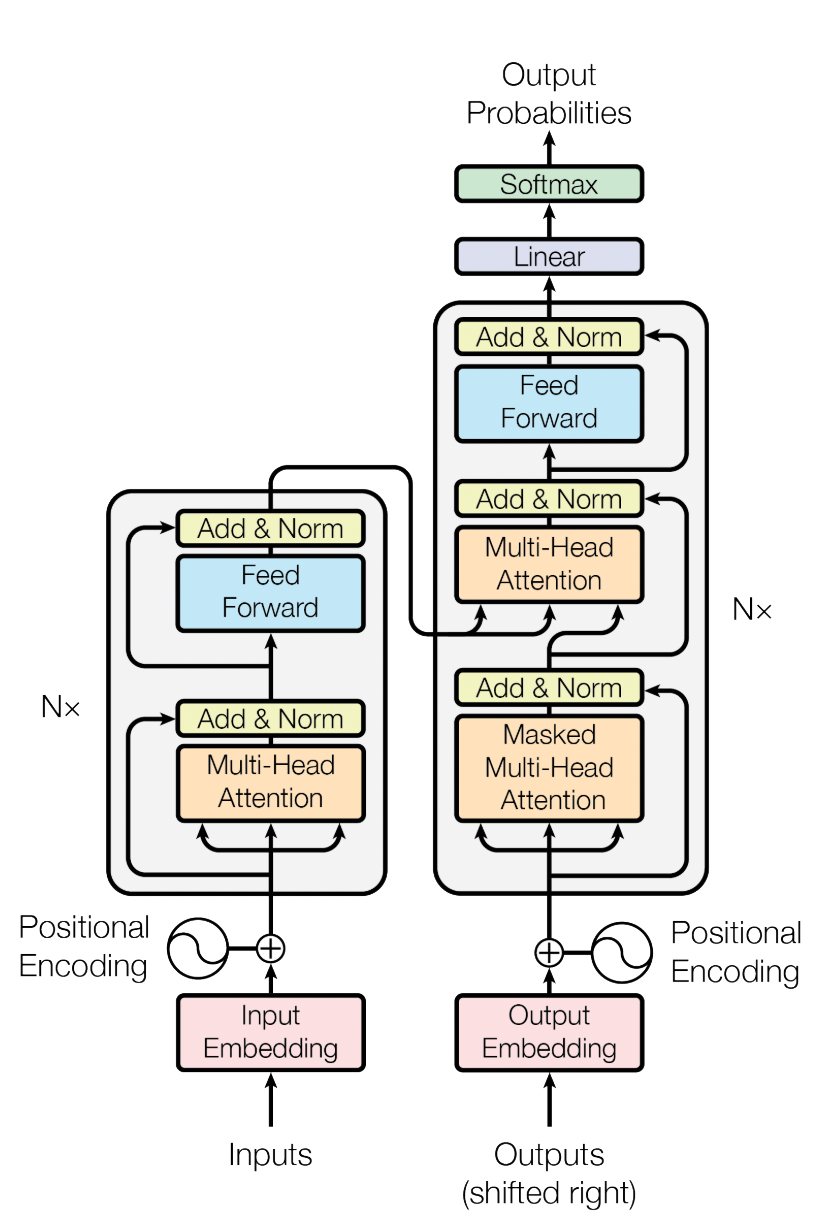
2.1 整体结构

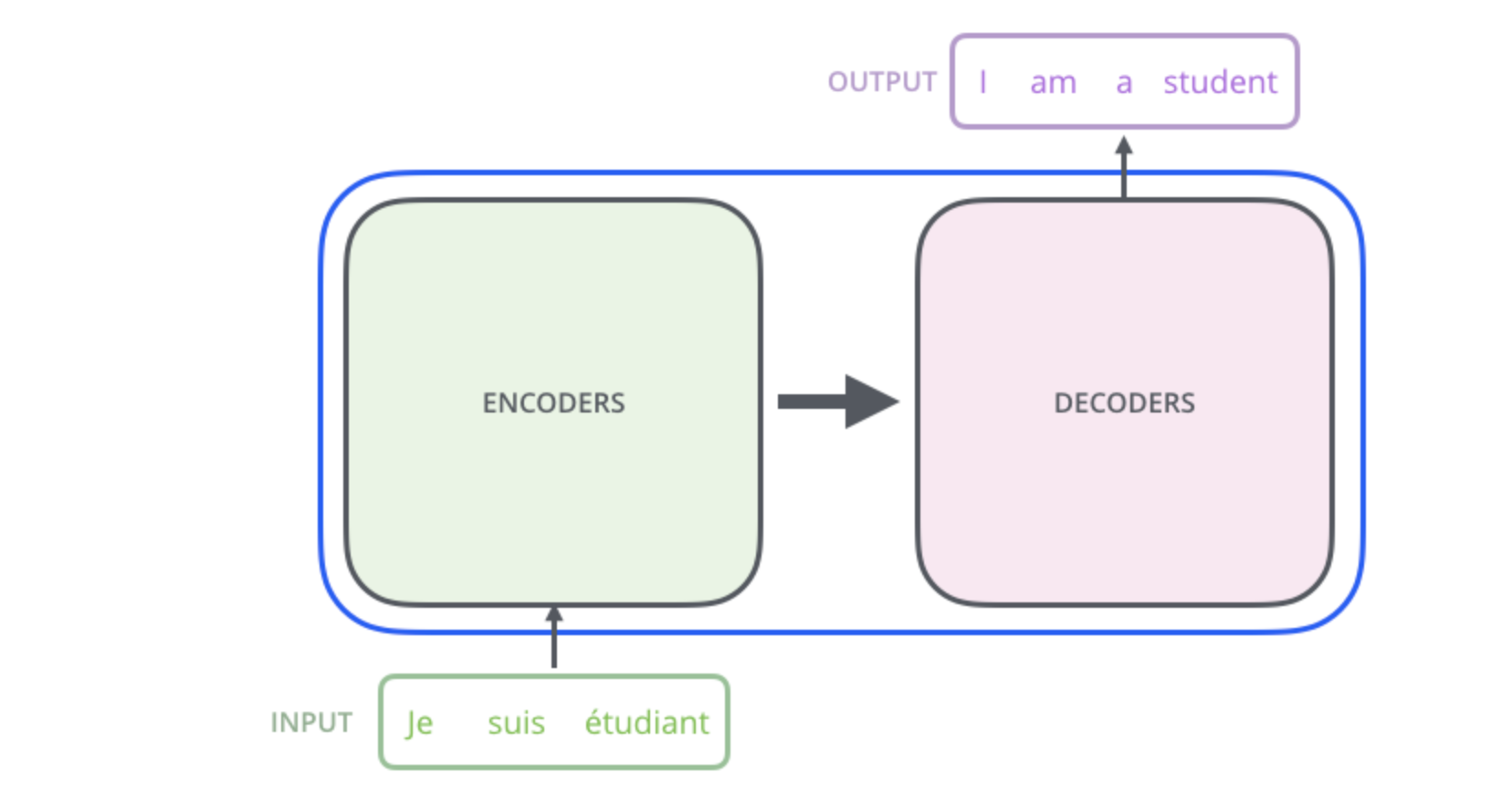
论文中是以机器翻译为例，输入数据先经过数据编码处理，先后经过encoder和decoder，最后输出结果。

因此整个模型包含三个子结构：

• 输入层
• Encoder层
• Decoder层

后面会对这三个子结构进行分析。

2.2 输入层

为了让输入的内容中可以包含对应的位置信息，在输入层中加入了位置编码。

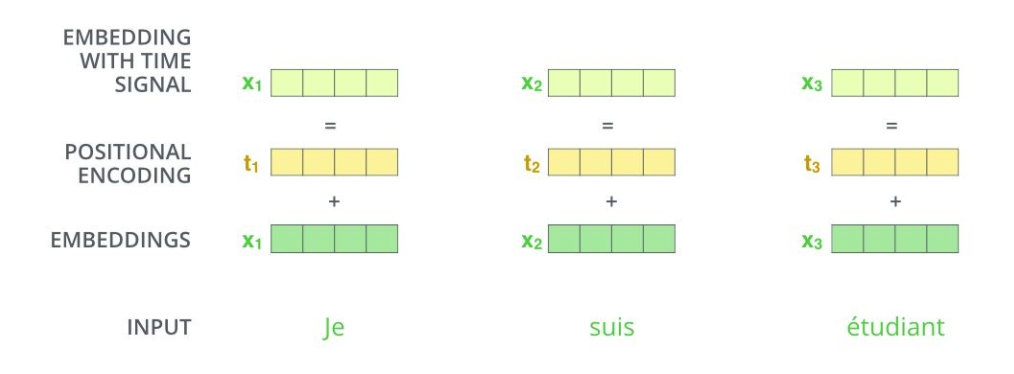
原始输入，首先通过word2vec或其他方式进行向量化，随后需要根据token的位置添加对应的位置向量。

位置向量的公式如下：

$\begin{array}{c} P E(p o s, 2 i)=\sin \left(\frac{p o s}{10000^{\frac{2 i}{d_{\text {model }}}}}\right) \\ P E(p o s, 2 i+1)=\cos \left(\frac{p o s}{10000^{\frac{2 i}{d_{\text {model }}}}}\right) \end{array}$

公式中的pos表示单词的位置，i表示单词的维度。这个位置向量的公式一方面可以表示单词的位置，同时还可以反应单词之间的相对位置：

$\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \\ \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$

位置为k+p的向量可以表示为位置k的特征向量的线性变化，可以捕捉到单词的相对位置。

另外，对于位置编码，作者提出了两种方式来表示：

1. 根据模型学习得到
2. 提前设定规则

transformer中使用了第二种方式，后续的bert模型则使用了第一种。

2.3 Encoder层

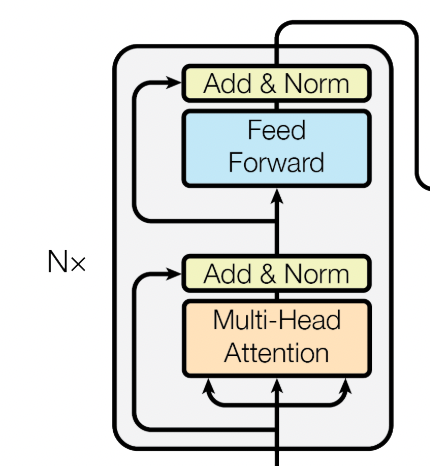
Encoder层中有N个encoder，这里以其中一个为例。

multi-head Attention

经过编码后的输入，首先会进入多头的注意力模型。

注意力模型可以简单理解为对每一个token，计算输入序列全部token对其的加权之和。具体的介绍在后面再介绍。

这里长度为(seq_len * hidden)的输入向量，经过多头注意力，维度依然为(seq_len * hidden)。

Feed Forward

经过attention计算之后的结果，再进入一个feed-forward netword.一共是2层线性变化外加一层非线性变化(relu)，公式如下：

$\mathrm{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2}$

Add&Norm

无轮是attention的输出，还是ffn的输出，都经过一个add和norm的处理。

其中add是指残差相加：x+F(x)。好处是对x求偏导的时候多了常数项1，连乘的时候不会造成梯度消失。

这里的norm是指layer norm，与batch norm的区别如图所示：

norm的作用都是将输入数据转为均值为0，方差为1的数据，目的是为了使数据落在激活函数的非饱和区，避免过拟合。

2.4 Decoder层

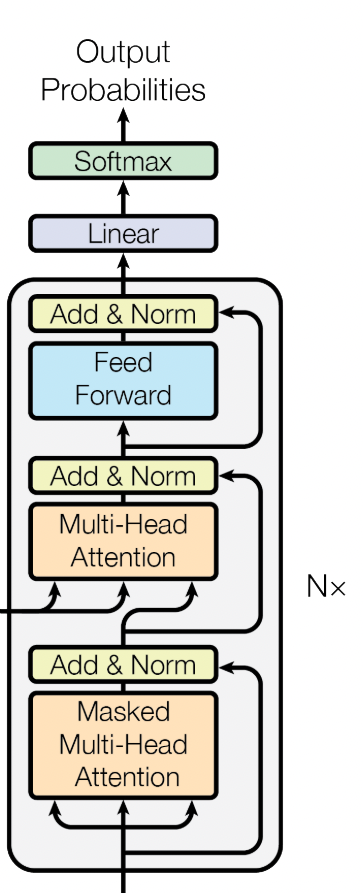
与encoder类似，decoder这里也是N个decoder拼在一起的。

以一层为例，这里输入数据到最后输出的顺序为 masked-多头self-attention,encoder-decoder-attention,FFN。

这里共经过了两个attention，区别如下：

• 第一个注意力结构为self-attention，但是加了mask
• 第二个注意力没有mask，但是不是self-attention。

具体的区别会在后续介绍。

经过N层decoder计算之后，输出的结果会接一个线性层，维度和vocabulary一样，再对这个结果做softmax。

3 注意力结构

Attention其实就是一个加权计算。

3.1 Scaled Dot-Product Attention

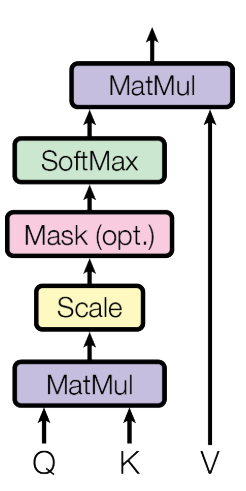
这里明确三个基本输入内容：

Q：Query

K：Key

V：Value

这三个都是向量，计算公式如下：

$\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V$

具体计算流程如下：

• 根据输入向量，生成q,k,v三个向量
• 为向量计算得分，score = q * k
• 为例梯度稳定，除以$\sqrt{d_{k}}$进行归一化
• 对归一化后的score进行softmax
• 结果点乘向量v,得到加权的每个输入向量的评分v
• 相加最终的结果 $z=\sum v$

这里的self-attention就是值q,k,v均来自同一个输入，如果不是不是来自同一个输入，依然可以计算attention。transformer中这三个向量是通过3个权重矩阵生成的

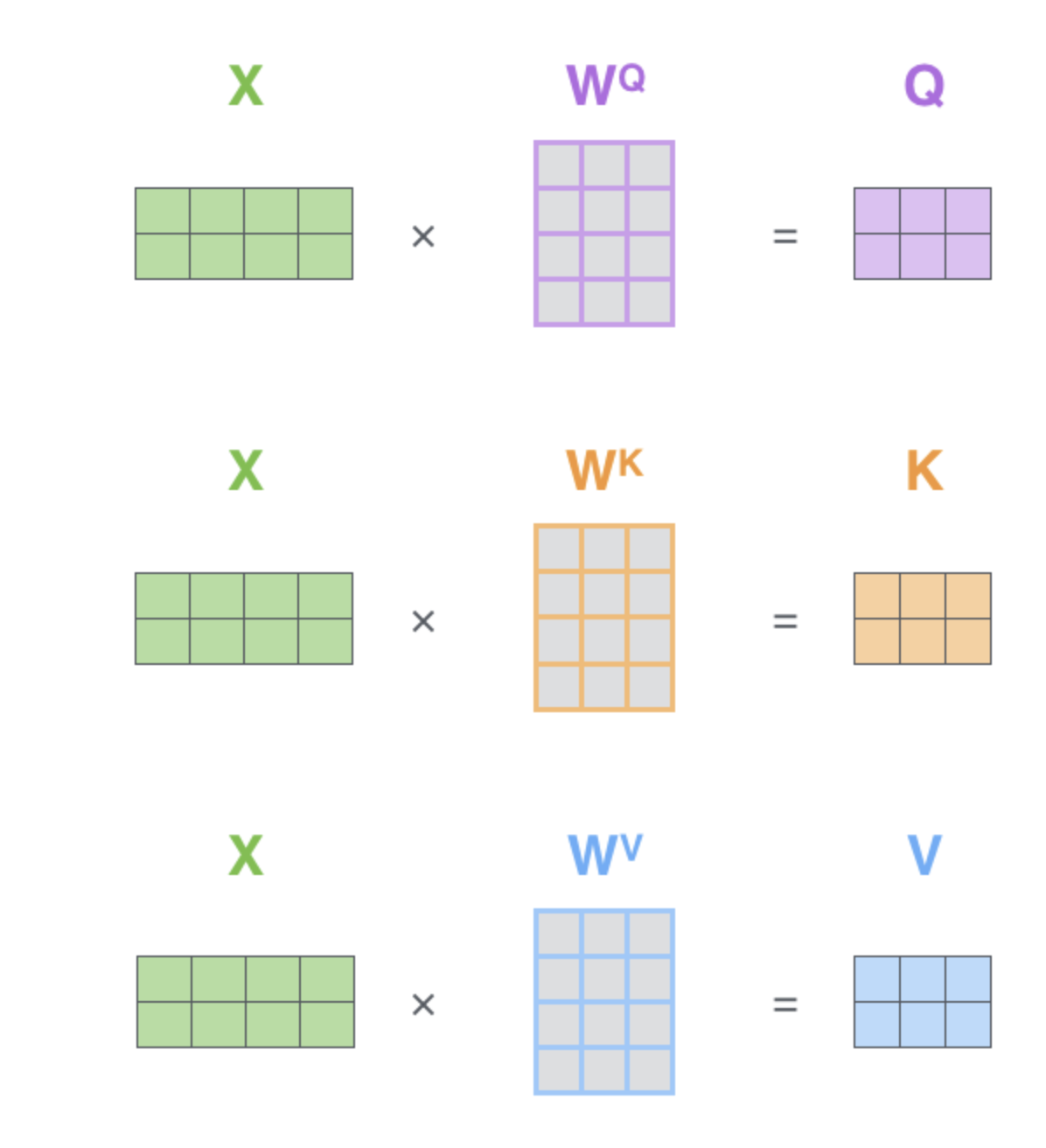
举个简单例子：

输入的句子为[我,爱,中国],计算“我”对应的attention值，需要分布计算我和整个句子里3个token的权重，这个权重再乘以对应的value，加权求和后的结果为“我”基于[我,爱,中国]的注意力值。

3.2 Multi-Head Attention

这transformer中，实际用到的是多头注意力结构。原理也很好理解，就是把多个attention的输出值concat成一个最终的输出。

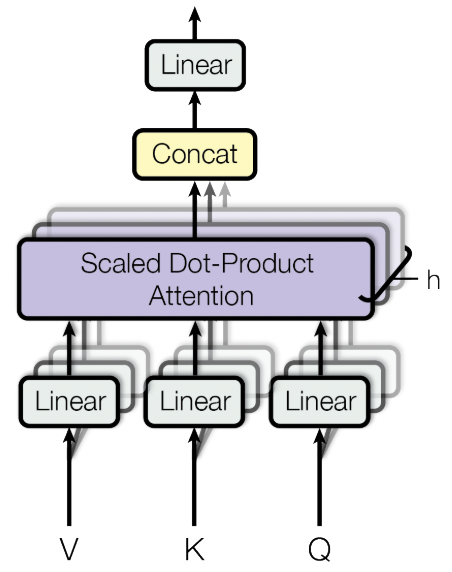
假设输入的维度为(batch,seq_len,hidden),对应的多头数量为n。

对于每一个head，输出的维度为(bath,seq_len,hidden/n)。最终再将多个head的结果拼接在一起作为最终输出。

多头的优点：

让模型去关注不同方面的信息，多头可以关注来自不同子空间的信息。

同时，根据论文的实验结果，多头的数量不是越多就一定越好。

3.3 attention中mask操作

attention中mask分成padding mask和sequence mask。

3.3.1 padding mask

论文中的三处attention都用到了padding mask。

主要是针对变长的序列，填充这些地方为0，避免影响计算。在实际实现是把对应位置的值填充为负无穷，这样softmax计算的时候就会忽略掉这些填充的位置。

操作： 通过index记录padding的起始位置，然后将对应位置的值填充为负无穷。 padding mask 是一个Boolen的张量，false就是padding的地方。把false填充为负无穷。

3.3.2 sequence mask

用来mask掉后面的信息。主要用在了 decoder层的self-attention中。

实现的方式，生成一个上三角矩阵，上三角的值为1，下三角和对角线设为0。作为attention-mask 后续做填充。

需注意：decoder层的self-attention 同时用到了这两种mask方法，具体实现是两个mask相加作为对应的mask。

decoder中使用mask的原因是因为在不想让当前的词看到后面的内容。

3.4 transformer中的三处attention

在encoder和decoder的过程中，共用到了3次attention

• encoder中self-attention。这里看成对输入的token进行全局的加权特征提取，获得最重要的特征。
• decoder中的self-attention。这里为了保证当前的token不会看到后面的内容，对后面的内容进行了mask。
• decoder中的encoder-decoder attention。这里的query来自于之前的decoder layer，key和value来自encoder的输出。

参考资料

Attention is all you need

The Illustrated Transformer

详解Transformer （Attention Is All You Need）