Max Blog

风控模型中常见的评估指标总结。

1.PSI

1.1 基本定义

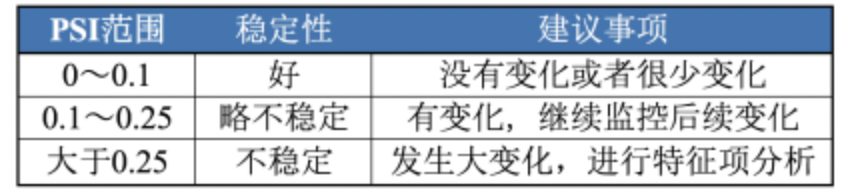
PSI反应测试集在各分数段和训练集分布的稳定性

$psi=\sum_{i=1}^{n} (A_i-E_i)*ln(A_i/E_i)$

PSI = SUM( (实际占比 - 预期占比）* ln(实际占比 / 预期占比) )

1.2 计算步骤

计算步骤：

• step1：将变量预期分布（excepted）进行分箱（binning）离散化，统计各个分箱里的样本占比。 注意：
• • a) 分箱可以是等频、等距或其他方式，分箱方式不同，将导致计算结果略微有差异；
  • b) 对于连续型变量（特征变量、模型分数等），分箱数需要设置合理，一般设为10或20；对于离散型变量，如果分箱太多可以提前考虑合并小分箱；分箱数太多，可能会导致每个分箱内的样本量太少而失去统计意义；分箱数太少，又会导致计算结果精度降低。
• step2: 按相同分箱区间，对实际分布（actual）统计各分箱内的样本占比。
• step3:计算各分箱内的A - E和ln(A / E)，计算index = (实际占比 - 预期占比）* ln(实际占比 / 预期占比)
• step4: 将各分箱的index进行求和，即得到最终的PSI

1.3 PSI与相对熵

相对熵(KL散度)公式：

$KL(P||Q)=-\sum{P(x)}log\frac{1}{P(x)}+\sum{P(x)}log\frac{1}{Q(x)} \\=\sum{P(x)}log\frac{P(x)}{Q(x)}$

用观察分布Q(x)去描述真实分布P(x)，还需要多少额外的信息量。

相对熵越小，两个概率越接近。类比PSI。

$psi=\sum_{i=1}^n(A_i-E_i)*ln(A_i/E_i)\\psi=\sum_{i=1}^nA_i*ln(A_i/E_i)+\sum_{i=1}^nE_i*ln(E_i/A_i)$

第1项：实际分布（A）与预期分布（E）之间的KL散度—— KL(A||E)

第2项：预期分布（E）与实际分布（A）之间的KL散度——KL(E||A)

从相对熵角度解释PSI:

对实际分布(A)与预期分布(E)的对称化相对熵之和。

1.4 业务应用

psi主要用来监测稳定性。包括已上线的模型稳定性和变量的稳定性。

Q：模型的KS保持较高的值，但是psi变大，如何评价模型？

以效果为评判标准，模型为好模型。PSI变大，只能说明当前样本与历史样本分布差异较大，不能直接说明模型变差。乐观解释：当前的客群相较之前变好。

所以，PSI只是一个稳定性的监测指标。

2.ROC

2.1 混淆矩阵

风控样本不均衡，正负比例悬殊。全部预测为负，准确率都很高。

使用混淆矩阵

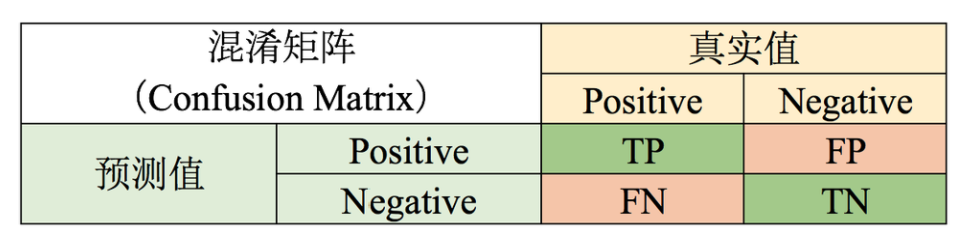
真阳率：TPR=TP/(TP+FN) --预测为正且正确的样本占所有正样本比例(抓对了)

假阳率：FPR=FP/(FP+TN) --预测为正且错误的样本占所有负样本比例(抓错了)

2.2 绘制流程

按分数升序排列，计算阈值下的TPR和FPR。因此，TPR可以看成累计正样本率，FPR可以看成累计负样本率。

在不同的阈值下，计算TPR和FPR。以FPR为横轴，TPR为纵轴。画出ROC曲线。曲线下方面积为AUC值。

2.3 曲线分析

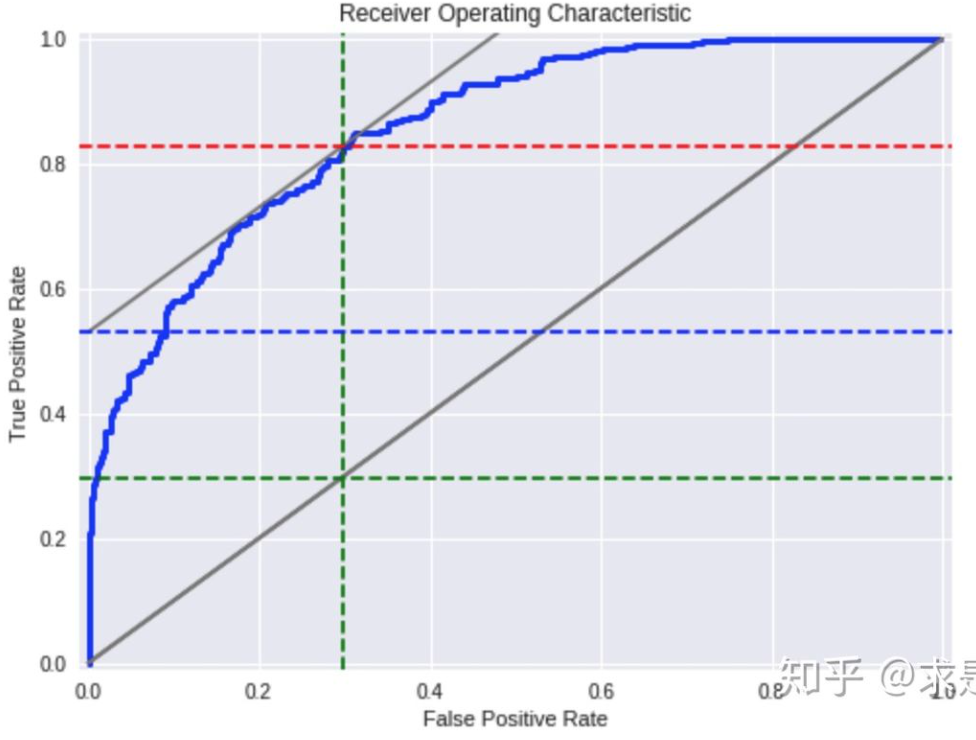
• 如果模型没有任何区分度，无论选取任何阈值进行划分，正样本都是均匀分布。最终曲线就是对角线。
• 实际模型的目标是最大化TPR同时最小化FPR。max(|TPR-FPR|)。与下一节的KS定义相同。
• 曲线越向左上角拉，说明模型的效果越好。

3.KS

ks的作为为衡量模型对正负样本的区分度。

3.1 区分度概念

对于自变量x与因变量y。通过对比正负样本的群体分布差异来表示区分度。

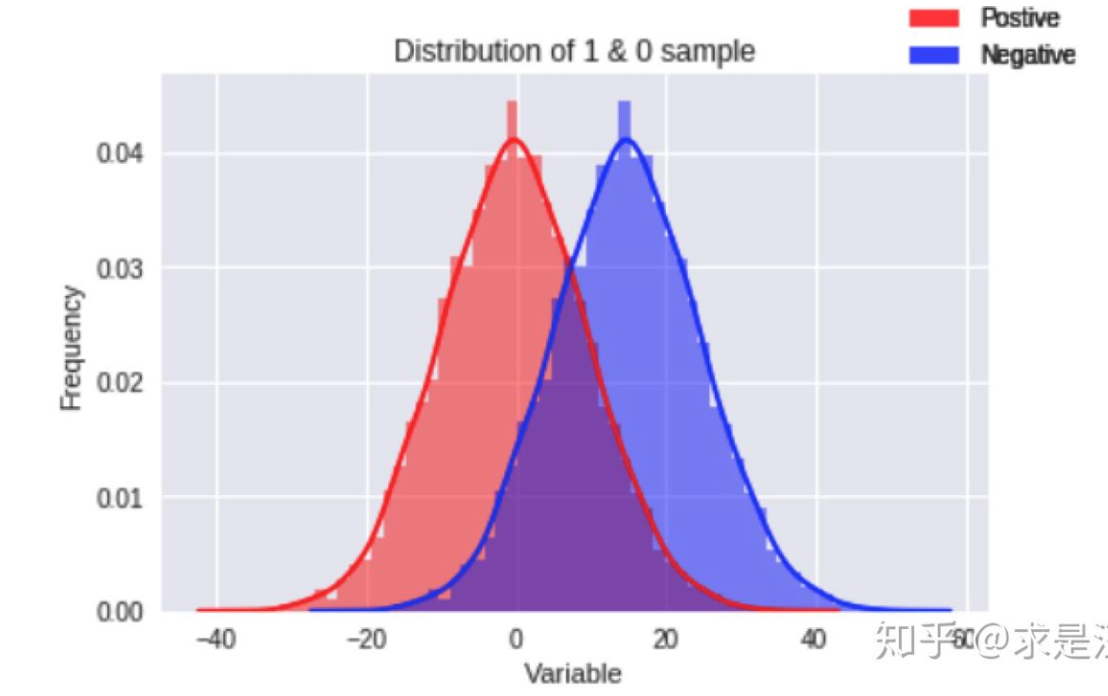
两个分布的重叠部分越小，正负样本的差异性越大。说明x能更好的把正负样本区分开。

区分度越大，说明模型越能分出好坏样本。

3.2 KS计算

$ks=max\{|cum(bad\_rate)-cum(good\_rate)|\}$

• step 1. 对变量进行分箱（binning），可以选择等频、等距，或者自定义距离。

• step 2. 计算每个分箱区间的好账户数(goods)和坏账户数(bads)。

• step 3. 计算每个分箱区间的累计好账户数占总好账户数比率(cum_good_rate)和累计坏账户数占总坏账户数比率(cum_bad_rate)。

• step 4. 计算每个分箱区间累计坏账户占比与累计好账户占比差的绝对值，得到KS曲线。

• step 5. 在这些绝对值中取最大值，得到此变量最终的KS值

因为是取最大值，所以KS值计算的好坏距离或区分度的上限。

3.3 KS分析

• KS的计算是基于放贷样本。放贷样本与申请样本存在偏差。偏差强弱与风控系统的效果成反比。裸奔的风控系统，两个样本之间几乎没有偏差。反之偏差很大。KS高不能100%说明模型效果一定好。
• KS的效果不佳。检验训练样本与测试样本的客群是否存在明显差异。
• 风控中y的取值为离散的，但是实际的定义应该是连续的。逾期10天为坏人。逾期9天为好人。【待补充】【为何选用KS】
• KS检验：检验两个分布是否相同。基本思路为计算最大偏离值，检验偏离值是否偶然出现。

3.4 KS与ROC的关系

• 如果希望增大KS，ROC曲线就越接近(0,1)。
• 如果KS保持不变，TPR与FPR同增同减，经典trade-off。增大TPR：抓对更多坏人。减少FPR：减少错抓的好人。 如何选择阈值，取决于实际业务。是高召回还是低误伤。

4.WOE与IV

4.1 基本定义

WOE: (Weight of Evidence）证据权重，通过特定编码方式对自变量进行编码。

IV: (Informmation Value) 信息价值,可以衡量自变量的预测能力，类似基尼系数。

WOE 描述了变量与二值target之间的关系，IV衡量这种关系的强弱。

简而言之，均是描述自变量与因变量关系的指标。

4.2 计算步骤

$WOE_i=ln(\frac{Bad_i}{Bad_T}/\frac{Good_i}{Good_T}) \\IV_i=(\frac{Bad_i}{Bad_T}-\frac{Good_i}{Good_T})*WOE_i \\IV=\sum_{i=1}^nIV_i$

• step 1. 对于连续型变量，进行分箱（binning），可以选择等频、等距，或者自定义间隔；对于离散型变量，如果分箱太多，则进行分箱合并。

• step 2. 统计每个分箱里的好人数(bin_goods)和坏人数(bin_bads)。

• step 3. 分别除以总的好人数(total_goods)和坏人数(total_bads)，得到每个分箱内的边际好人占比(margin_good_rate)和边际坏人占比(margin_bad_rate)。

• step 4. 计算每个分箱里的 $ WOE=In( \frac{margin_bad_rate}{margin_good_rate} ) $

• step 5. 检查每个分箱（除null分箱外）里woe值是否满足单调性，若不满足，返回step1。

  注意：null分箱由于有明确的业务解释，因此不需要考虑满足单调性。

• step 6. 计算每个分箱里的IV，最终求和，即得到最终的IV。
  备注：好人 = 正常用户，坏人 = 逾期用户

需要注意：

1. 分箱时需要注意样本量充足，保证统计意义。
2. 若相邻分箱的WOE值相同，则将其合并为一个分箱。
3. 当一个分箱内只有好人或坏人时，可对WOE公式进行修正如下：

$WOE_i=ln(\frac{Bad_i+0.5}{Bad_T+0.5}/\frac{Good_i}{Good_T})$

4.3 IV与PSI对比

讲IV公式展开，对比PSI

$IV=\sum_{i=1}^n(\frac{Bad_i}{Bad_T}-\frac{Good_i}{Good_T})*ln(\frac{Bad_i}{Bad_T}/\frac{Good_i}{Good_T})$

$psi=\sum_{i=1}^n(\frac{A_i}{A_T}-\frac{E_i}{E_T})*ln(\frac{A_i}{A_T}/\frac{E_i}{E_T})$

两者形式上是一致的。结合1.3，可以用相对熵对IV进行解释。

IV是从信息熵上比较好人分布于坏人分布之间的差异性。

对比PSI：

• PSI衡量预期分布于实际分布之间的差异。IV对比好人坏人分布的差异。
• PSI判断变量的稳定性。IV判断变量的预测能力。

IV高的变量不代表入模效果一定好，反之一样。