Max Blog

线性回归算法的基本内容总结

1 线性基函数模型

回归问题的最简单模型是输入变量的线性组合

$y(\mathbf x,\mathbf w) = w_0+w_1x_1+...+w_Dx_D \tag{1.1}\\ 其中，\mathbf x = (x_1,x_2,...x_D)^T$

线性回归模型的关键性质是它是参数$w_0,...,w_D$​的一个线性函数。同时，也是输入变量$x_i$的一个线性函数。

因为线性回归同时是参数和输入变量的线性函数，给模型带来了较大的局限性。可以通过基函数，对模型进行拓展：

$y(\mathbf x,\mathbf w) = w_0 + \sum_{j=1}^{M-1}w_{j}\phi_{j}(x) = \mathbf w^{T} \boldsymbol{\phi(x)} \tag{1.2}\\ 其中，\mathbf w = (w_0,...w_{M-1})^T,\boldsymbol{\phi} = (\phi_0,...\phi_{M-1})^T,\phi_0(x)=1$

通过使用非线性的基函数，可以使函数$y(x,w)$​​成为输入向量x的一个非线性函数。但是，模型依然可以被称为线性模型，因为这个函数是参数w的线性函数。通过基函数，去拟合非线性的x。通常情况下，可以默认$\phi(x)=x$。

一些常见的基函数有多项式基函数、高斯基函数、sigmoid基函数、傅里叶基函数等。

通过$sin(2\pi x)$​​​与高斯随机噪声随机生成一批样本，如果使用多项式函数作为基函数对样本数据进行处理，再进行线性回归拟合，随着多项式阶数的增加，拟合效果会越来越好，甚至过拟合。

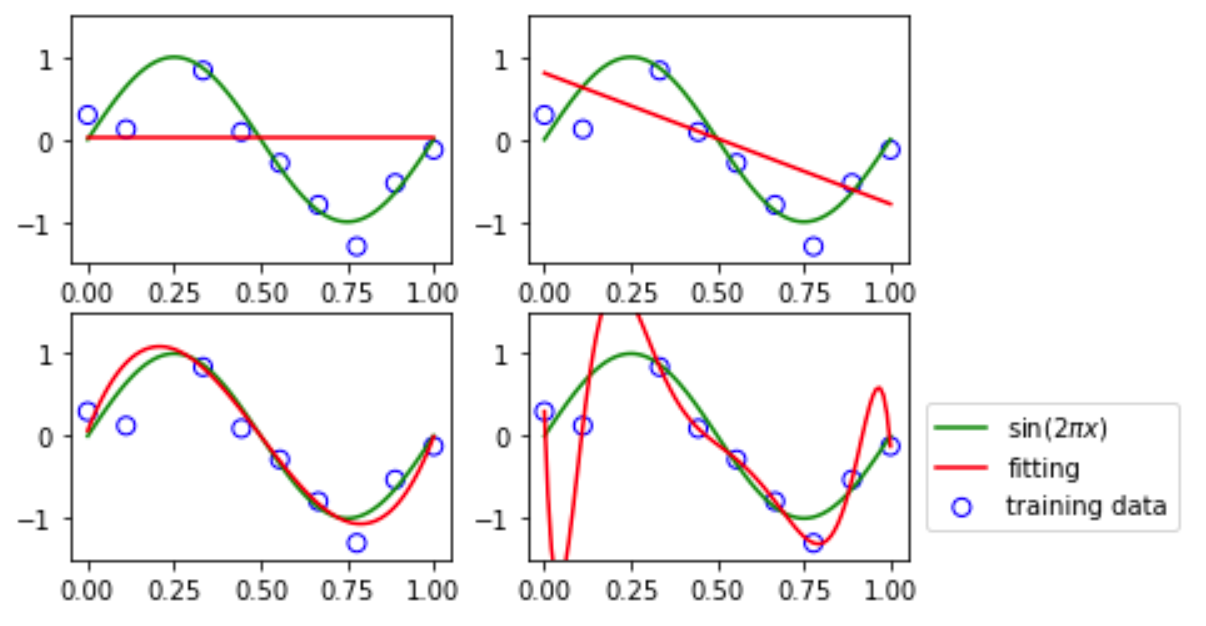从左到右，分别对应多项式阶数为0，1，3，9时曲线

上图可以看出，对于非线性的变量x，通过多项式基函数，可以使用线性回归模型可以对其进行拟

2 最大似然和最小平方

假设目标变量t由函数$y=(x,w)$给出，且函数被附加了高斯噪声，则t满足：

$t = y(x,w) + \epsilon \tag{2.1}$

其中$\epsilon$是一个均值为0的高斯随机变量，精度(方差的倒数)为$\beta$​,联合公式1.1可得：

$p(t|x,w,\beta) = \mathcal N(t|y(x,w),\beta^{-1}) \tag{2.2}$

将输入的数据集$\mathbf X = {x_1,...,x_N}$和对应目标值$\mathbf t = {t_1,...,t_N}$​，以向量的形式进行表示，并假设数据点事独立的从分布(1.4)中抽取，则似然函数的表达式为：

$p(t|X,w,\beta) = \prod_{n-1}^{N}\mathcal N(t_n|w^T\phi(x_n),\beta^{-1}) \tag{2.3}$

取似然函数的对数，公式转化为：

$\begin{aligned} \ln p(\mathbf{t} \mid \boldsymbol{w}, \beta) &=\sum_{n=1}^{N} \ln \mathcal{N}\left(t_{n} \mid \boldsymbol{w}^{T} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right), \beta^{-1}\right) \\ &=\frac{N}{2} \ln \beta-\frac{N}{2} \ln (2 \pi)-\beta E_{D}(\boldsymbol{w}) \end{aligned} \tag{2.4}$

Q1:为什么使用对数似然函数？

1.对似然函数取对数不影响单调性

2.似然函数是概率的连乘，结果容易趋于零，不利于计算。

# 创建一些概率很小的样例
>>> p = np.random.random_sample((100,)) * 0.000001

# 取对数
>>> log_p = [np.log(x) for x in p]
# 计算似然连乘结果
>>> np.product(p)
0.0

# 计算对数似然累加结果
>>> np.sum(log_p)
-1482.3811696310242

其中，平方和误差函数为公式中的最后一项：

$E_{D}(\boldsymbol{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{t_{n}-\boldsymbol{w}^{T} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right)\right\}^{2} \tag{2.5}$

这里也变相解释了为什么线性回归使用平方和误差作为损失函数。

接下来，会基于公式2.4，对其中的参数进行求解。

根据对数似然函数，使用最大似然方法确定w和$\beta$​。基于公式1.6可以发现，在噪声服从高斯分布的情况下，最大化模型的似然函数等价于最小化平方和误差函数。对公式1.7进行求梯度：

$\nabla \ln p(\mathbf{t} \mid \boldsymbol{w}, \beta)=\beta \sum_{n=1}^{N}\left\{t_{n}-\boldsymbol{w}^{T} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right)\right\} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right)^{T} \tag{2.6}$

令梯度为0，

$0=\sum_{n=1}^{N} t_{n} \phi\left(\boldsymbol{x}_{n}\right)^{T}-\boldsymbol{w}^{T}\left(\sum_{n=1}^{N} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right) \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right)^{T}\right)\tag{2.7}$

求得参数w的解析解：

$\boldsymbol{w}_{M L}=\left(\mathbf{\Phi}^{T} \boldsymbol{\Phi}\right)^{-1} \boldsymbol{\Phi}^{T} \mathbf{t}\tag{2.8}$

其中：

$\boldsymbol{\Phi}=\left(\begin{array}{cccc} \phi_{0}\left(\boldsymbol{x}_{1}\right) & \phi_{1}\left(\boldsymbol{x}_{1}\right) & \cdots & \phi_{M-1}\left(\boldsymbol{x}_{1}\right) \\ \phi_{0}\left(\boldsymbol{x}_{2}\right) & \phi_{1}\left(\boldsymbol{x}_{2}\right) & \cdots & \phi_{M-1}\left(\boldsymbol{x}_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{0}\left(\boldsymbol{x}_{N}\right) & \phi_{1}\left(\boldsymbol{x}_{N}\right) & \cdots & \phi_{M-1}\left(\boldsymbol{x}_{N}\right) \end{array}\right) \tag{2.9}$

如果默认$\mathbf{\Phi}=\mathbf{X},\mathbf{t}=\mathbf{y}$,则参数w的公式则为常见的

$\boldsymbol{w}_{M L}=\left(\mathbf{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T} \mathbf{Y}\tag{2.10}$

理论上，模型的参数w可以通过解析解个公式求得。在实际中，通常使用梯度下降的方法逼近求解。

Q2：为什么有了解析解，还需要使用梯度下降的方法求解？

(1)解析解公式中涉及逆矩阵求解，X可能没有逆矩阵(X的秩<X的维度)，导致无解
(2)样本数量和样本维度较多时，求解速度慢

如果对公式2.6中的参数w进行展开，则公式变为：

$E_{D}(\boldsymbol{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{t_{n}-w_{0}-\sum_{j=1}^{M-1} w_{j} \phi_{j}\left(\boldsymbol{x}_{n}\right)\right\}^{2}\tag{2.11}$

对$w_0$求导，令其导数为0，结果为：

$w_{0}=\bar{t}-\sum_{j=1}^{M-1} w_{j} \bar{\phi}_{j}\tag{2.12}$

其中，

$\bar{t}=\frac{1}{N} \sum_{n=1}^{N} t_{n}, \quad \bar{\phi}_{j}=\frac{1}{N} \sum_{n=1}^{N} \phi_{j}\left(\boldsymbol{x}_{n}\right)\tag{2.13}$

偏置参数$w_0$​,补偿了目标值的平均值和基函数输出值的平均值的差值。

类比关于参数w的似然函数，基于公式1.6，对噪声精度参数$\beta$进行最大化似然函数，结果为：

$\frac{1}{\beta_{M L}}=\frac{1}{N} \sum_{n=1}^{N}\left\{t_{n}-\boldsymbol{w}_{M L}^{T} \boldsymbol{\phi}\left(\boldsymbol{x}_{n}\right)\right\}^{2}\tag{2.14}$

噪声精度的导数$\frac{1}{\beta}$,其值由目标值和估计值的残差给出。​

3 最小二乘法的几何描述

接下来从几何的角度来描述最小平方。

首先从线性方程组开始，

给定两个线性方程组，

$\left\{\begin{array}{l} x_{1}+x_{2}=3 \\ -x_{1}+x_{2}=1 \end{array}\right.\tag{3.1}$

将上式转换成矩阵的形式，可以表示为：

$\begin{aligned} &{\left[\begin{array}{l} 1 \\ -1 \end{array}\right] \times x_{1}+\left[\begin{array}{l} 1 \\ 1 \end{array}\right] \times x_{2}=\left[\begin{array}{l} 3 \\ 1 \end{array}\right]} \\ &\uparrow \qquad \qquad \qquad\uparrow \qquad \qquad\uparrow \\ &a_{1} \quad \times \quad x_{1}+a_{2} \times x_{2}=b \end{aligned} \tag{3.2}$

可以理解为向量a1的x1倍加上向量a2的x2倍，等于向量b,在坐标系中如图所示：

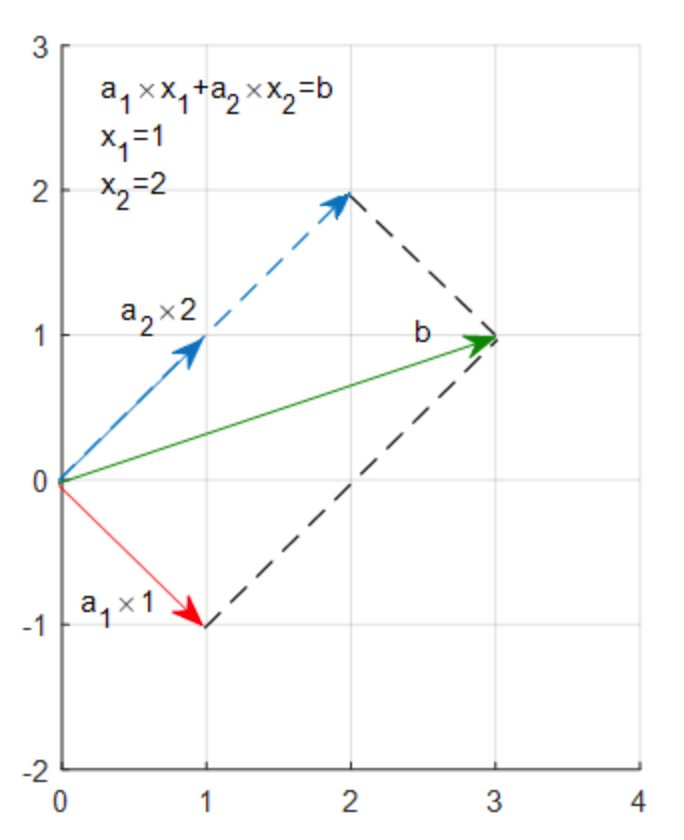
向量a1的1倍加上向量a2的2倍，刚好等于向量b。对应的倍数1，2就是对应的解$x_1,x_2$​。

从列的角度看线性方程，Ax=b的解，就是找到A里的列向量的一个线性组合，使之等于b。

以上是针对有解的线性方程组。

对于无解的线性方程组，可以通过最小二乘法就是来求解。

假设平面上有3个点，P1(1,2),P2(0,2),P3(2,3)。现在用一条y = kx +b的直线去拟合三个点，如果直线可以通过这三个点，则意味着以下的方程组有解：

$\left\{\begin{array}{l} 1 \times k+b=2 \\ 0 \times k+b=2 \\ 2 \times k+b=3 \end{array}\right.\tag{3.3}$

但发现无法找到一条直线同时通过三个点

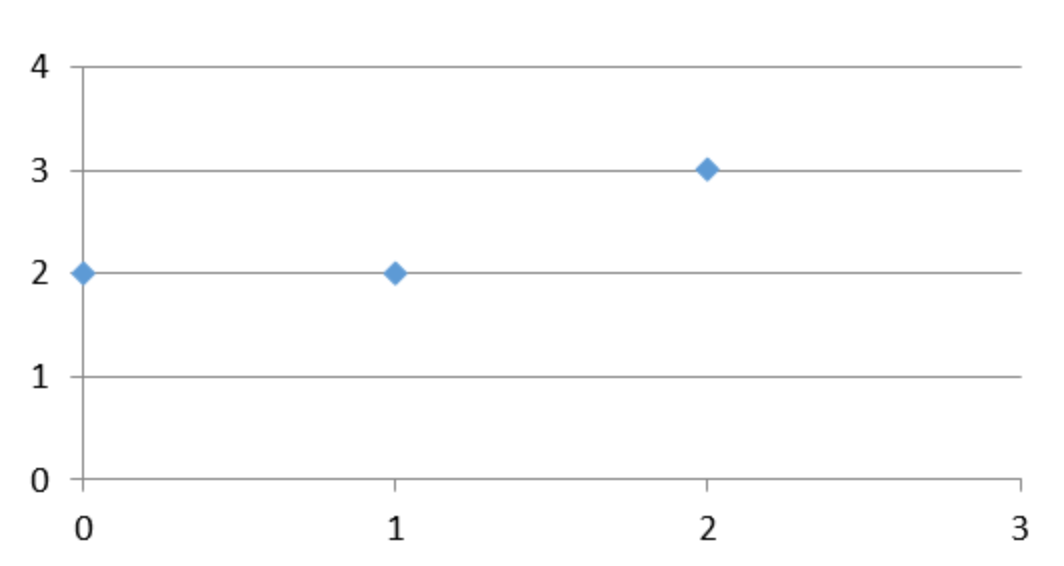
下面为了拟合这三个点，对k和b进行求解。以$x_1表示k,以x_2表示b$,方程组如下：

$\left\{\begin{array}{l} 1 \times x_{1}+x_{2}=2 \\ 0 \times x_{1}+x_{2}=2 \\ 2 \times x_{1}+x_{2}=3 \end{array}\right.\tag{3.4}$

转换为矩阵相乘的形式为：

$\left[\begin{array}{l} 1 \\ 0 \\ 2 \end{array}\right] \times x_{1}+\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] \times x_{2}=\left[\begin{array}{l} 2 \\ 2 \\ 3 \end{array}\right] \Leftrightarrow a_{1} \times x_{1}+a_{2} \times x_{2}=b\tag{3.5}$

将对应向量放在空间坐标系中，如下图所示，发现无法在$a_1,a_2$确定的平面中组合出一条向量，使这条向量刚好等于b(向量b不在$a_1,a_2$所在的平面S上)。

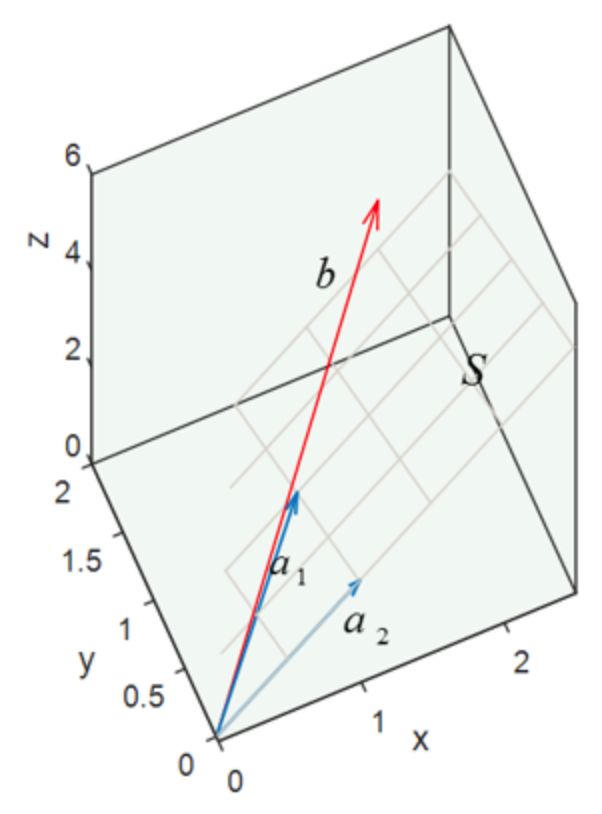
因为无法找到完美的解，退而求此次，找一个最接近的解。因此方程组的求解思路转换为：在平面S上找一个最接近向量b的向量来代替向量b。

向量b在平面S上的投影，即为要找的替代向量P。P与b之间的误差为$e=b−P$

原方程组($Ax=b$​)是无解的，在使用P替代b之后，方程组($A\hat{x}=P$​)有解。

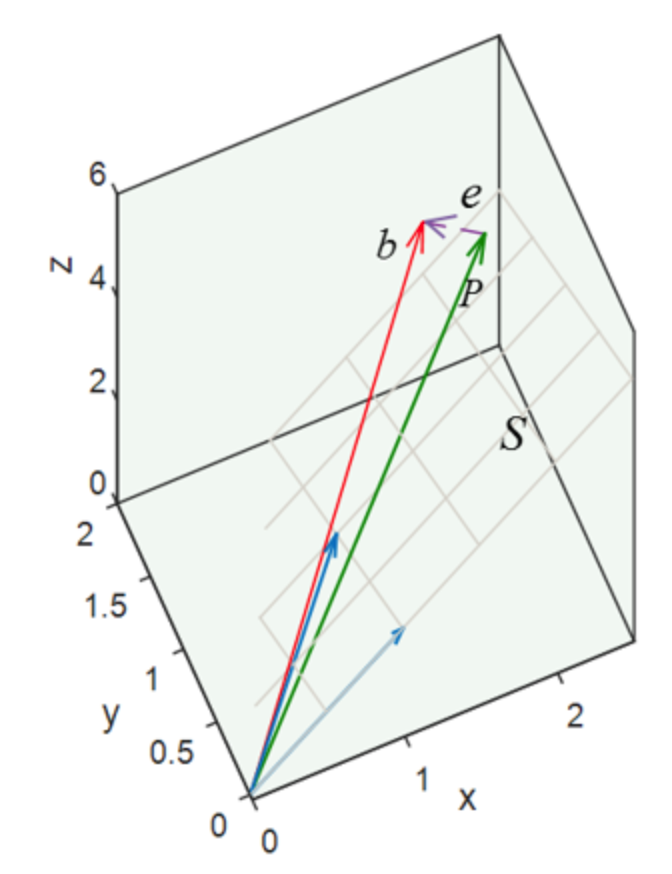
此时，误差最小，且误差正交于平面S。因此，向量e于向量$a_1，a_2$的点乘均为0。

$\begin{gathered} A^{T} e=0 \\ A^{T}(b-A \hat{x})=0 \end{gathered} \tag{3.6}$

解得：

$\hat{x}=\left(A^{T} A\right)^{-1} A^{T} b \tag{3.7}$

求出k和b以后，得到拟合曲线。

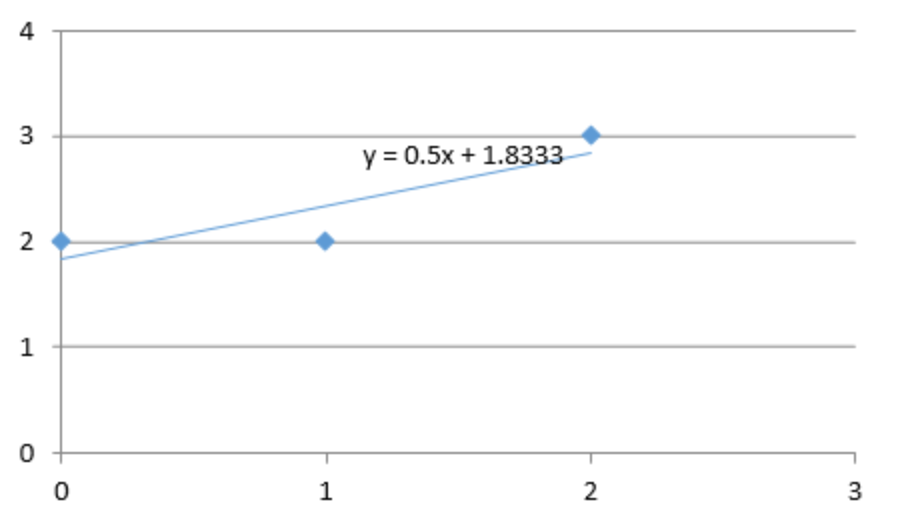
回顾刚才的流程，对于无法求得精确解的线性方程组，通过投影的形式表示误差，从而求解，得到方程组的近似解。

结论：最小二乘法的几何意义就是高维空间中的一个向量在低维子空间的投影。

4 正则化

为了减少过拟合，会通过添加正则项的方法来控制过拟合。因此需要最小化的总误差项的形式变为：

$E_{D}(\boldsymbol{w})+\lambda E_{W}(\boldsymbol{w})\tag{4.1}$

将公式4.1展开，则带正则化的误差函数形式为：

$\frac{1}{2} \sum_{n=1}^{N}\left\{t_{n}-\boldsymbol{w}^{T} \boldsymbol{\Phi}\left(\boldsymbol{x}_{n}\right)\right\}^{2}+\frac{\lambda}{2} \sum_{j=1}^{M}\left|w_{j}\right|^{q}\tag{4.2}$

当q=1时，对应一次正则化项，整个线性回归函数也被称为套索回归(Lasso Regression)。

当q=2时，对应二次正则化项，整个线性回归函数也被称为岭回归(Ridge Regression)。

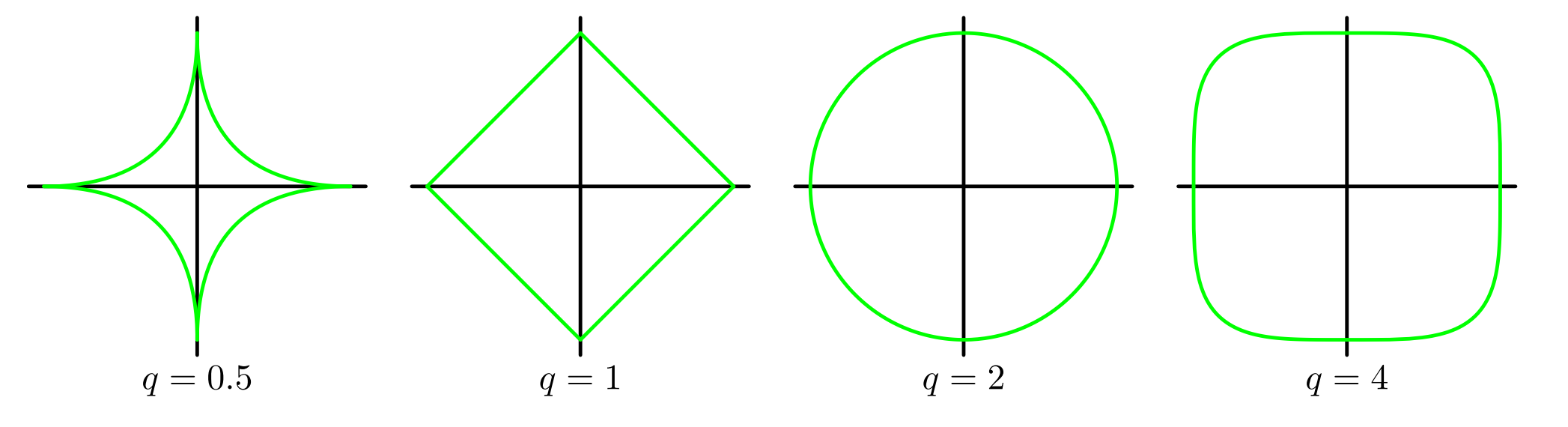对于不同的参数q,1.25中正则化项的轮廓线

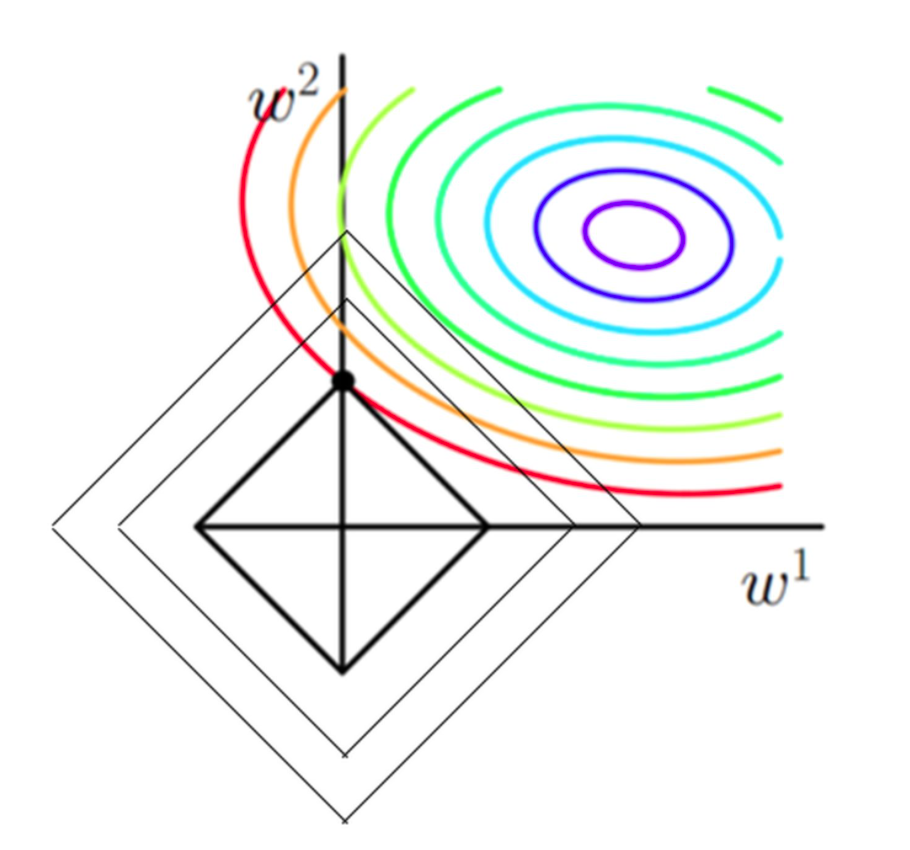带L1正则化的目标函数求解

图中的等高线可以看为公式1.24的第一部分，在同一颜色的等高线下，损失函数的值相同。在不考虑正则项的情况下，对函数进行优化，最终结果是等高线最里面的紫色线上的点。

以L1正则为例，$L_1=|W_1|+|W_2|$的图像刚好是一个菱形，菱形上的值表示对应的L1的值相等。目前的优化目标除了使等高线中的值要小(越接近紫色线)，同时也要使菱形的值越小(菱形越小)。

在等高线不变的情况下(以红色等高线为例)，可以与菱形有多种交点。等高线与菱形相切的时候，对应的菱形要小于等高线与菱形相割的情况。这个相切的交点，表示在误差项相同的情况下，正则项最小，从而总误差最小。

为什么 L1比L2容易得到稀疏解？

优化问题角度

对公式4.1的的求最小化，可以看成优化问题：

$\begin{array}{ll} \min _{\boldsymbol{w}} &E_{D}(\boldsymbol{w}) \\ \text { s.t. } & \lambda E_{W}(\boldsymbol{w}) \leq \eta \end{array} \tag{4.3}$

其中$\eta$是自行设定的容忍度$E_{D}(\boldsymbol{w})$是经验风险，$E_{W}(\boldsymbol{w})$​是正则化项，。此优化问题可以描述为：把w的解限制在一定范围内，同时使得经验风险尽可能小。L1与L2的正则化图像如下所示：

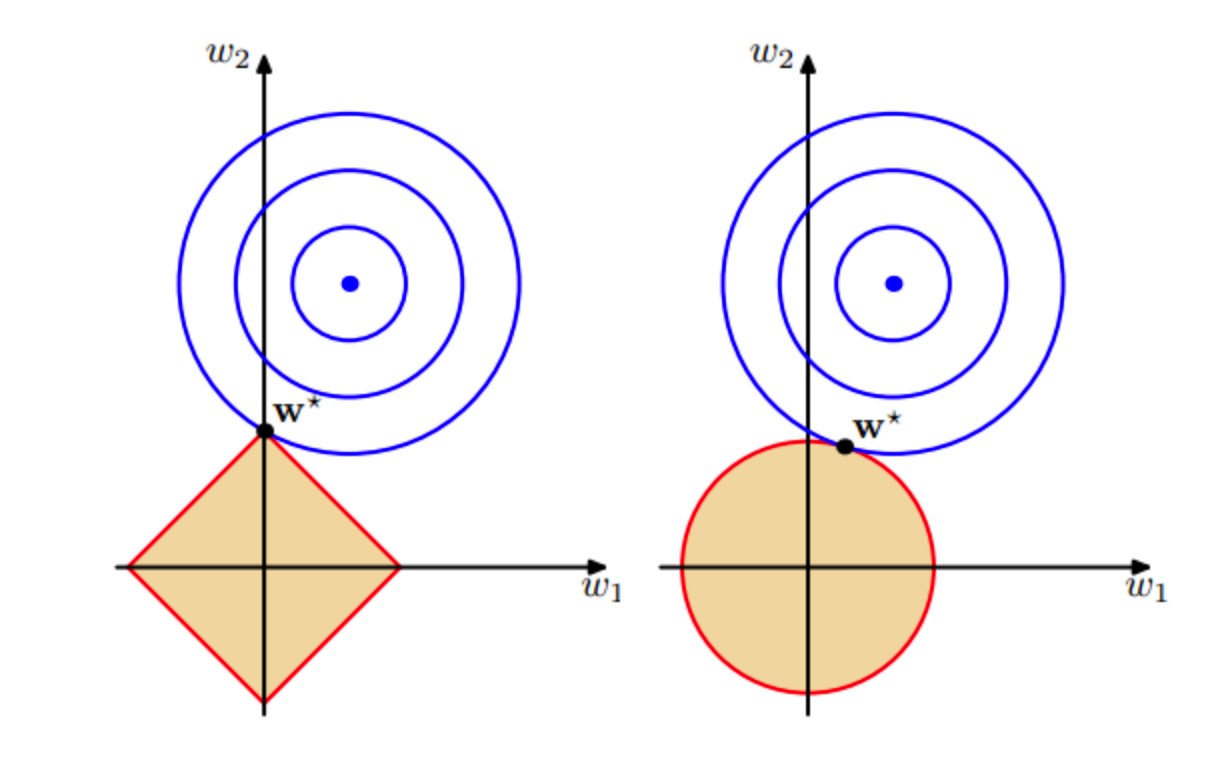
从图中可以看出，L1正则化相比于L2正则化更容易使得切点落在w某个维度$w_i$的坐标轴上，从而导致另一个维度$w_j$的取值为0，从而更容易得到具有稀疏性的w。

梯度角度

L1正则对应的损失函数为：

$J(\boldsymbol{w})=L(\boldsymbol{w})+\lambda \sum\left|w_{i}\right| \tag{4.4}$

L2正则对应的损失函数为：

$J(\boldsymbol{w})=L(\boldsymbol{w})+\lambda \sum\left(w_{i}\right)^{2} \tag{4.5}$

分别对参数w的某个维度$w_i$求偏导，

对公式4.4求偏导：

$\frac{\partial J(\boldsymbol{w})}{\partial w_{i}}=\frac{\partial L(\boldsymbol{w})}{\partial w_{i}}+\lambda \operatorname{sign}\left(w_{i}\right) \tag{4.6}$

对公式4.5求偏导：

$\frac{\partial J(\boldsymbol{w})}{\partial w_{i}}=\frac{\partial L(\boldsymbol{w})}{\partial w_{i}}+2 \lambda w_{i} \tag{4.7}$

当使用梯度下降法对参数进行更新的时候，

L1正则化中w的某个维度$w_i$的更新公式为：

$w_{i}:=w_{i}-\eta \frac{\partial J(\boldsymbol{w})}{\partial w_{i}}=w_{i}-\eta \frac{\partial L(\boldsymbol{w})}{\partial w_{i}}-\eta \lambda \operatorname{sign}\left(w_{i}\right) \tag{4.8}$

L2正则化中w的某个维度$w_i$​的更新公式为：

$w_{i}:=w_{i}-\eta \frac{\partial J(\boldsymbol{w})}{\partial w_{i}}=w_{i}-\eta \frac{\partial L(\boldsymbol{w})}{\partial w_{i}}-2 \eta \lambda w_{i} \tag{4.9}$

对比公式4.8和公式4.9，只看两个公式中的最后一项，L1参数更新时每次会减去恒定的$\eta \lambda$，即使$w_i$已经很小了，梯度依然变化较大，这使得$w_i$容易取得0值。L2参数更形时，减去的的值$2 \eta \lambda w_{i}$​与$w_i$有关，当$w_i$很小时，变化的梯度也很小，相较L1不容易取到0。

贝叶斯角度

对于概率模型的训练过程，实际是参数估计的过程。

对于参数估计，频率主义学派认为参数虽然未知，但客观存在且固定，可以通过优化似然函数来确定参数。常见的方法为极大似然估计(Maximum Likelihood Estimation，MLE)。

贝叶斯学派认为参数是未观察到的随机变量，本身也有分布，需要先假设参数服从一个先验分布，再基于观察到的数据来计算参数的后验分布。常见的方法为最大后验估计(Maximum A Posteriori，MAP)。

最大后验法的思路如下：

$\hat{\boldsymbol{w}}=\underset{\boldsymbol{w}}{\arg \max } P(\boldsymbol{w} \mid D) \tag{4.10}$

结合贝叶斯公式

$P(\boldsymbol{w} \mid D)=\frac{P(D \mid \boldsymbol{w}) P(\boldsymbol{w})}{P(D)} \tag{4.11}$

可得：

$\begin{aligned} \hat{\boldsymbol{w}} &=\underset{\boldsymbol{w}}{\arg \max } \frac{P(D \mid \boldsymbol{w}) P(\boldsymbol{w})}{P(D)} \\ &=\underset{\boldsymbol{w}}{\arg \max } P(D \mid \boldsymbol{w}) P(\boldsymbol{w}) \\ &= {\arg \max }(\prod_{i}P(Y_{i}|X_{i},w)\prod_{i}P(w)) \\ &= \operatorname{argmin}\left(\sum_{i}\left\|f\left(X_{i}\right)-Y_{i}\right\|^{2}+\sum_{i} \ln \left(P\left(w_{i}\right)\right)\right) \end{aligned} \tag{4.12}$

当参数的先验服从拉普拉斯分布时：

$P\left(w_{i}\right)=\frac{\lambda}{2} \exp \left(-\lambda\left|w_{i}\right|\right) \tag{4.13}$

带入公式4.12，可得

$\left.\hat{\boldsymbol{w}}=\operatorname{argmin}_{w}\left(\sum_{i}\left\|f\left(X_{i}\right)-Y_{i}\right\|^{2}+\lambda \sum_{i}\left|w_{i}\right|\right)\right) \tag{4.14}$

由公式4.14可知，当参数先验服从拉普拉斯分布时，最大后验估计=极大似然估计+L1正则化项。

当参数的先验服从高斯分布时：

$P\left(w_{i}\right)=\frac{\lambda}{\sqrt{\pi}} \exp \left(-\lambda\left\|w_{i}\right\|^{2}\right)\tag{4.15}$

带入公式4.12，可得

$\left.\hat{\boldsymbol{w}}=\operatorname{argmin}_{w}\left(\sum_{i}\left\|f\left(X_{i}\right)-Y_{i}\right\|^{2}+\lambda \sum_{i}\left\|w_{i}\right\|^{2}\right)\right) \tag{4.16}$

由公式4.14可知，当参数先验服从高斯分布时，最大后验估计=极大似然估计+L2正则化项。

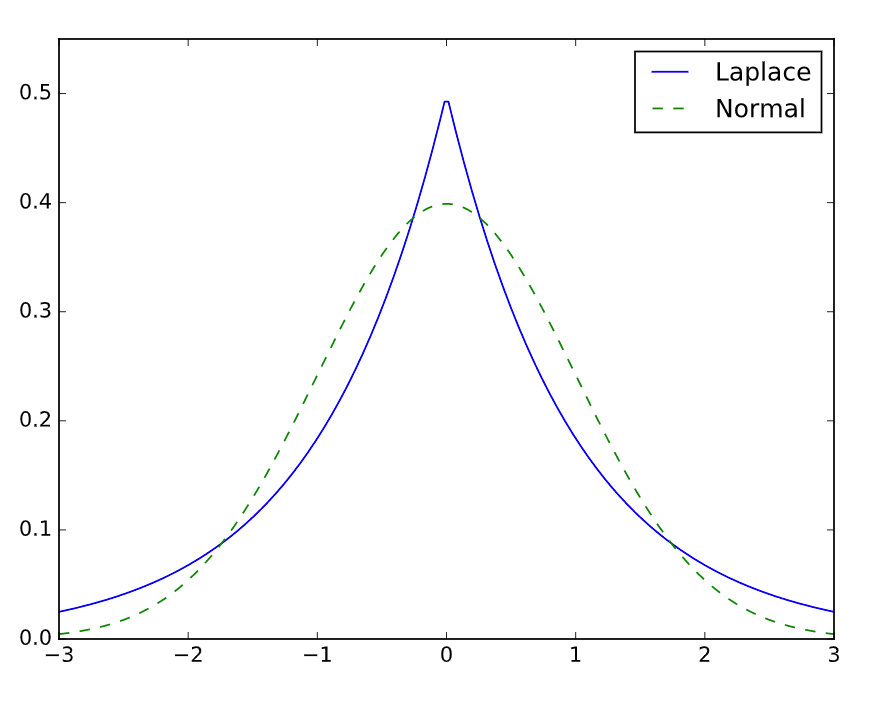
观察两个分布的概率密度函数图，拉普拉斯分布更为稀疏，取到0的概率更大，所以对应的参数w也更稀疏。

5 贝叶斯估计

5.1 贝叶斯与最大似然估计

在分析L1正则化为什么稀疏中，提到贝叶斯派的人认为，被估计的参数本身也服从一种分布。因此在估计参数时需要考虑参数分布的先验知识。在数据量小的情况下，引入先验知识后的结果往往更合理。基于参数的先验分布，也有最大后验法和贝叶斯估计两种思路。

由公式4.11可知，参数的后验分布为：

$P(\theta \mid D)=\frac{P(D \mid \theta) P(\theta)}{P(D)} \tag{5.1}$

最大后验法：

认为参数是一个常数，能够找到最大化产生观测数据的参数。

在参数估计阶段，最大后验的目标是$\theta^{*}=\operatorname{argmax}_{\theta} P(D \mid \theta) P(\theta)$​。

预测阶段，通过确定的最佳参数对新数据进行预测。

贝叶斯估计：

参数是一个随机变量，参数估计阶段会通过先验分布和实际观测数据得到后验分布$P(\theta|D)$​​。

在预测新数据阶段，所有参数都会参与预测，但不同的参数权重($P(\theta|D)$​​)不同,各参数的预测结果加权。

	最大似然估计	最大后验	贝叶斯估计
目标	从观测数据找到最优参数$\theta^{*}$	从观测数据和先验分布中，找到最优参数$\theta^{*}$	从观测数据和先验分布中，找到后验分布 $P(\theta \vert D)$
预测形式	$P(X^{new}\vert \theta^{*})$	$P(X^{new}\vert \theta^{*})$	所有参数参与预测：$P\left(X^{\text {new }} \mid D\right)=\int P\left(X^{\text {new }} \mid \theta, D\right) P(\theta \mid D) d \theta$

例：

假设你想对一支股票的价格做预测，打算咨询身边的10个朋友($\theta$​)。

最大似然估计：

看了朋友们最近5次的预测记录(D)，找了预测最准的朋友张三($\theta^{*}$)做预测。

最大后验：

除了看了朋友们最近5次的预测记录(D),同时了解了大家与预测股票公司的关系($P(\theta)$).

最终选了在那家公司任职的朋友李四($\theta^{*}$​)做预测。

贝叶斯估计：

在看了朋友们最近5次的预测记录(D),和大家与预测股票公司的关系($P(\theta)$)之后，对大家的预测水平分配了权重$P(\theta |D)$。

在预测时，让所有人都参与预测，再根据实现计算好的权重，对所有人的预测结果做加权求和，作为最终的结果。

5.2 贝叶斯顺序学习

贝叶斯学习是一个顺序的过程，原本的后验，在看到一些新的数据后，会变成接下来未知数据的先验。在整个数据集上，整个过程是一个迭代的过程。

下图展示了贝叶斯估计的参数更新过程

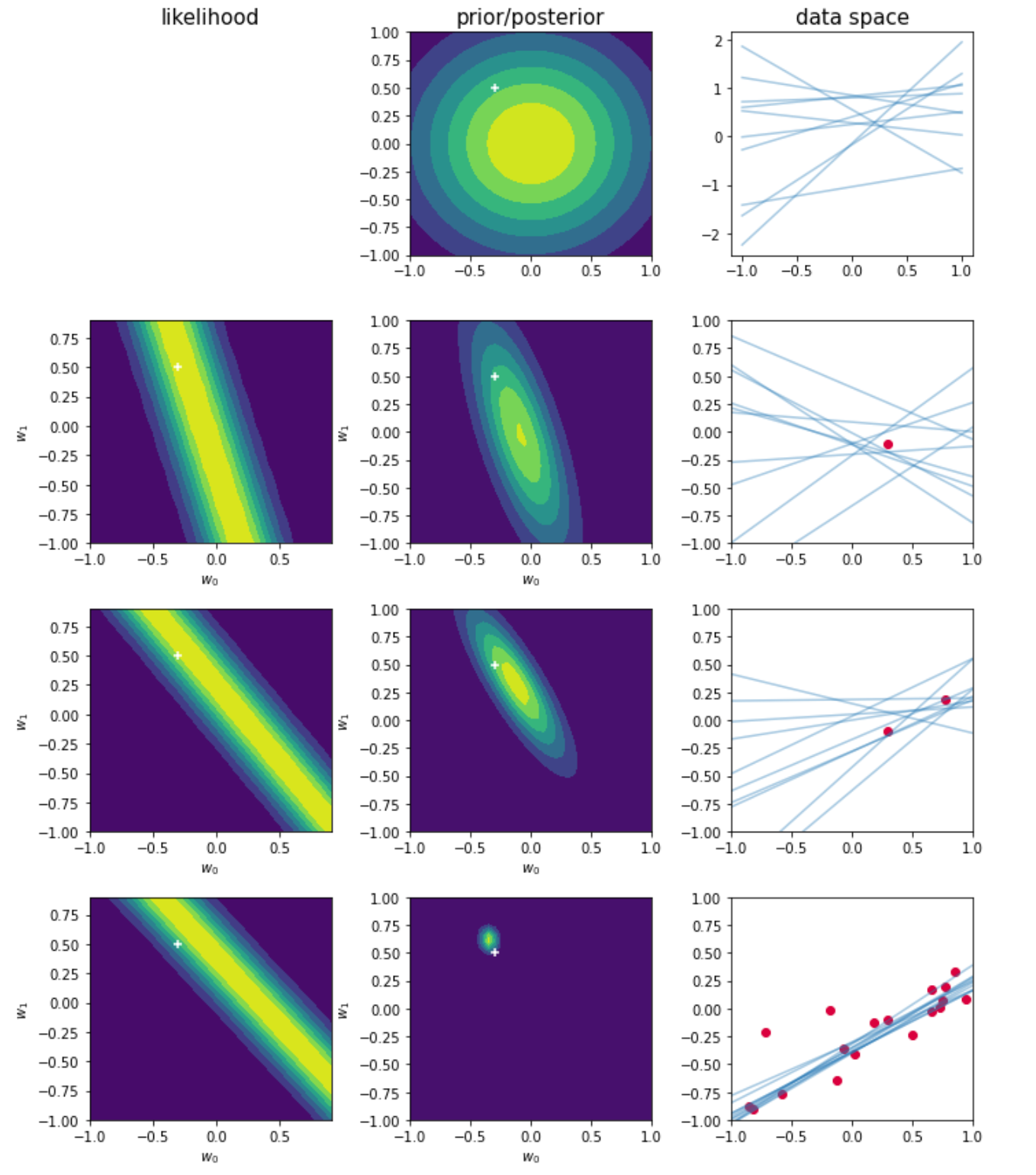
图中为$y(x,w) = w_0+w_1x$的线性模型，只有两个参数可以调节。

第一行对应于观测到任何数据点之前，给出了参数w的先验概率。第三列中蓝色曲线来自函数y(x,w)。这些曲线的w都是从先验概率中抽取的。

第二行，观测到了一个实际数据点(第三列)，第一列为基于这个观测到的数据的似然函数$p(y,w)$​关于w的函数图像。把这个似然函数与第一行中的先验概率(第二列)相乘，归一化后就得到了第二列中概率分布。这个图为当前w的后验分布。基于这个后验分布，可以生成新的一批蓝色曲线(第三列)。这些点大部分都穿过了观测点或观测点附近。

第三行，当观测到第二个点后，之前的后验分布(第二行第二列)此刻成了先验分布，与观测到两个点后似然函数(第三行第一列)相乘后，得到了当前的后验分布(第三行第二列)。基于此后验分布，生成了新的直线。

第四行，当观测到若干数据点后，后验概率变得十分尖锐，随着观测点数的增加，整个参数也在不停进行迭代学习。

6 参考资料

[1] Pattern Recognition and Machine Learning

[2] Mathematics for Machine Learning

[3] gerdm-prml