Max Blog

对GAN论文的笔记整理

Abstract

本文提出了一个新的模型框架。同时训练两个模型：一个生成模型G，用来获取训数据的分布；一个判别模型D，用来预测数据来自训练样本而不是G生成样本的概率。训练G的目的是尽可能让D犯错，让其无法判断一个数据是生成的还是来自训练样本。模型的框架类似于一个minimax 双人游戏。当任意函数 G 和 D的空间，存在一个特殊的解，G 恢复出训练数据的分布，D 在任何地方都等于 1/2 。在G和D由多层感知器定义的情况下，整个系统可以通过反向传播进行训练。

1 Introduction

深度学习目前发展的很好。到目前为止，在深度学习中最显著的成功涉及到判别模型，通常是那些将高维、丰富的感官输入映射到类标签的模型。这原因主要是基于反向传播和dropout算法，使用分段线性单元(piecewise linear units)，具有特别良好的梯度。深度生成模型的影响较小，原因在于在极大似然估计和相关策略中出现的许多难以处理的概率计算的近似性，以及由于难以在生成环境中利用分段线性单元的优点。因此，提出了生成对抗网络(Generative Adversarial Nets)。

在提出的对抗网框架中，生成模型与对手进行了比较:一个学习确定样本是来自模型分布还是来自数据分布的判别模型。

论文中提到的生成模型和判别模型，构成了对抗网络。其中这两个模型均可以使用bp和dropout来训练。整个过程中并不需要马尔科夫链。

2 Related work

主要讲了之前生成模型相关的一些工作。

• 在之前，大部分在deep generative model上的工作都是希望能够得到一个参数化的概率分布，可以通过最大似然估计进行学习，比较成功的模型有deep Boltzmann machine等。
• 之前比较类似的工作是VAE，即使用encoder将训练数据映射到高斯分布中，再使用decoder将其变换到原始的训练数据，从而实现对数据的参数化分布表示。

3 Adversarialnets

符号说明：

• 生成器分布：$p_{g}$

• 数据集：$x$

• 输入噪声变量：$p_{z}(z)$

• 将噪声变量映射到数据空间：$G(z;\theta_{g})$

  G为多层感知器，参数为$\theta$,可微

• 另一个多层感知器：$D(x;\theta_{d})$

  $D(x)$:$x$来自数据集而不是$p_{g}$的概率

我们训练D，使其能够最大程度的将正确的标签分配给训练数据和G生成的样本。

同时，我们训练G，使得$log(1-D(G(z)))$最小。

换句话说，G和D正在进行value function为$V(G,D)$的two-player minimax game：

$\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]$

训练过程中无法先先练好D，再去训练G，因此每训练k步的D网络，再训练一步G网络。

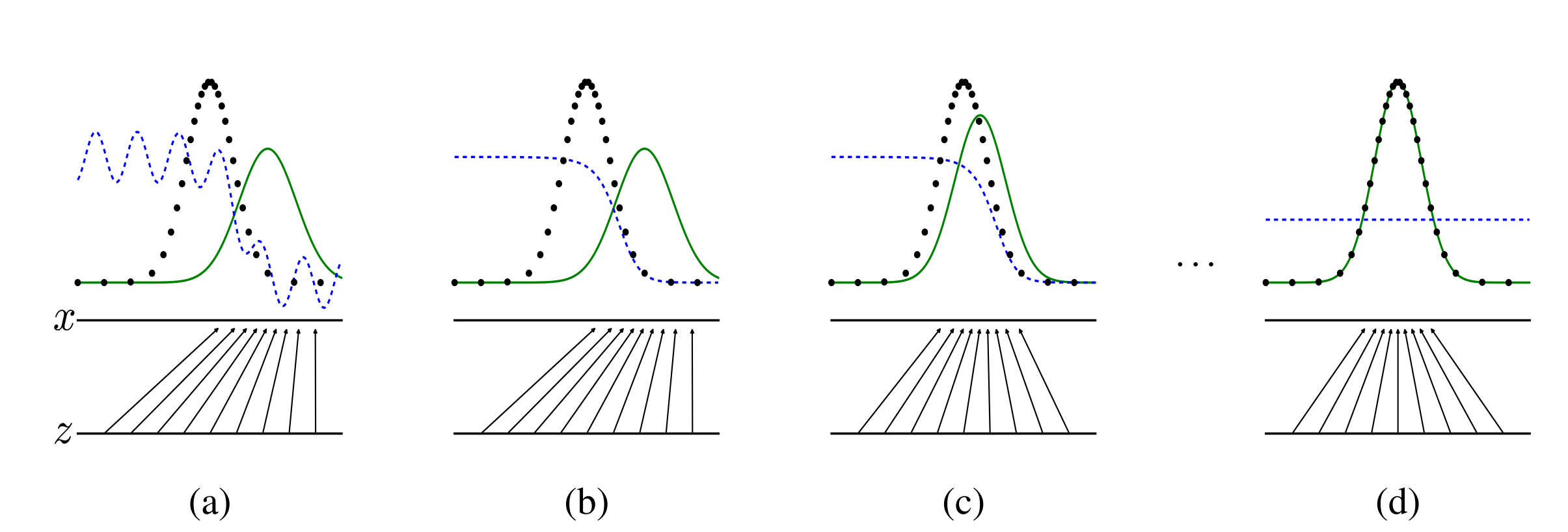
黑色线为真实的样本分布情况。绿色线表示生成的样本分布情况。

蓝色的虚线表示判别器判别概率的分布情况。

z表示噪声，平行线表示z映射到x。

模型的目的是让绿色曲线去拟合黑色曲线，从而使得判别器无法正确的判断。

• (a) 考虑一个接近收敛的对抗情况：$p_{g}$与$p_{data}$相似，D是一个比较准确的分类器。
• (b) 在算法的循训练过程中，D被训练从数据中区分样本，$D^{*}(x)=\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$
• (c) 对G进行更新后，D的梯度会指引$G(z)$向更容易分类为正常数据的方向更新
• (d) 经过多步的训练后，G和D会到达一个双方均无法提升的位置。因为$p_{g}=p_{data}$,鉴别器无法区分这两个分布，最终$D(x)=\frac{1}{2}$​

算法流程：

4 Theoretical Results

当$z$ ~ $p_{z}$时，G生成的数据分布为$p_{g}$。当模型容量和数据足够的情况下，希望G生成的数据分布能够很好的拟合$p_{data}$。

对于提到的极大极小算法，全局优化的目标为$p_{g}=p_{data}$。

对于前面提到的生成器G和判别器D，下面的目的是证明两者可以求得最优解。

目标函数：

$V(G, D)=\log (D(x))+\log (1 - D(G(z))$

最好的鉴别器：

目标是为了V(G,D)最大，即：

$D_{G}^{*}=\operatorname{argmax}_{D} V(G, D)$

最好的生成器：

当鉴别模型取最好的情况下，最好的生成模型是想把目标函数最小

$G_{D}^{*}=\operatorname{argmin}_{G}\left(\operatorname{argmax}_{D} V(G, D)\right)$

因此，问题转化成了最大最小问题:

$\min _{G} \max _{D} V(G, D)=E_{x \sim p_{\text {data }}(x)} \log (D(x))+E_{x \sim p_{z}(z)} \log (1-D(G(z))$

以下为对这个问题是否有最优解的证明

证明有最优鉴别模型D

$V(G, D)=E_{x \sim p_{\text {data }}(x)} \log (D(x))+E_{x \sim p_{z}(z)} \log (1-D(G(z))$

$V(G, D)=\int_{x} p_{\text {data }}(x) \log (D(x))+p_{g}(x) \log (1-D(x)) d x$

为简化公式，以a,b,y替换$p_{data},p_{g}(x),D(x)$,公式简化为：

$f(y)=a \log y+b \log (1-y)$

解得：

$f^{\prime}(y)=0 \Rightarrow \frac{a}{y}-\frac{b}{1-y}=0 \Rightarrow y=\frac{a}{a+b}$

因此证明：

$\begin{aligned} &V(G, D)=\int_{x} p_{\text {data }}(x) \log D(x)+p_{G}(x) \log (1-D(x)) \mathrm{d} x \\ &\quad \leq \int_{x} \max _{y} p_{\text {data }}(x) \log y+p_{G}(x) \log (1-y) \mathrm{d} x \end{aligned}$

鉴别器的最优解为：

$D(x)=\frac{p_{\text {data }}}{p_{\text {data }}+p_{G}}=\frac{1}{2}$

证明生成器有最优解：

证明：

当且仅当，$p_{G}=p_{data}$​时，$C(G)=maxV(G,D)$可以取得最小值

充分性：

$V\left(G, D_{G}^{*}\right)=\int_{x} p_{\text {data }}(x) \log \frac{1}{2}+p_{G}(x) \log \left(1-\frac{1}{2}\right) \mathrm{d} x =-\log 2 \int_{x} p_{G}(x) \mathrm{d} x-\log 2 \int_{x} p_{\text {data }}(x) \mathrm{d} x=-2 \log 2=-\log 4$

必要性：

$C(G)=\int_{x} p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)+p_{G}(x) \log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \mathrm{d} x$

$\begin{gathered} C(G)=\int_{x}(\log 2-\log 2) p_{\text {data }}(x)+p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \\ +(\log 2-\log 2) p_{G}(x)+p_{G}(x) \log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \mathrm{d} x \\ C(G)=-\log 2 \int_{x} p_{G}(x)+p_{\text {data }}(x) \mathrm{d} x \\ +\int_{x} p_{\text {data }}(x)\left(\log 2+\log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \\ +p_{G}(x)\left(\log 2+\log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \mathrm{d} x \end{gathered}$

$\begin{gathered} C(G)=\int_{x}(\log 2-\log 2) p_{\text {data }}(x)+p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \\ +(\log 2-\log 2) p_{G}(x)+p_{G}(x) \log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \mathrm{d} x \\ C(G)=-\log 2 \int_{x} p_{G}(x)+p_{\text {data }}(x) \mathrm{d} x \\ +\int_{x} p_{\text {data }}(x)\left(\log 2+\log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \\ +p_{G}(x)\left(\log 2+\log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \mathrm{d} x \end{gathered}$

上式转化为KL散度：

$C(G)=-\log 4+K L\left(p_{\text {data }} \mid \frac{p_{\text {data }}+p_{G}}{2}\right)+K L\left(p_{G} \mid \frac{p_{\text {data }}+p_{G}}{2}\right)$

因为后面的KL散度大于0，所以目标函数最终的最优质值为$-log4$

通过以上证明，证明了生成器和鉴别器可以取得最优解。

后面第4.2节同时证明了算法的收敛性，如果G和D都有足够的容量，则在每次迭代过程中，D都会到达其最优解，之后在更新G的时候，G都会进行优化，使得$p_{g}$向$p_{data}$收敛

5 Advantages and disadvantages

缺点：

模型对应$p_{g}$没有一个显性的表示

模型在训练过程中D和G需要共同训练，共同优化参数。如果只训练其中一个效果比较差。

优点：

不需要马尔科夫链，只用bp就可以训练模型

可以在模型中嵌入很多其他函数

总结

提出了通过生成器和鉴别器共同训练的思路，是整个论文的核心。

参考资料

Generative Adversarial Nets

An Annotated Proof of Generative Adversarial Networks with Implementation Notes

Generative Adversarial Nets论文解读