概率校准笔记

概率校准的介绍和常见的方法

1. 定义

1.1 概率校准

模型输出的概率未必等于实际的概率。比如模型输出0.8，理想情况下应该说明这个事情发生的概率为80%。但在分类模型中，有可能输出0.8并不表示发生的概率为80%。

概率校准就是对分类函数做出的分类概率进行重新计算。

1.2 原因分析

模型输出的概率不准确经常出现在风控等场景中。主要原因与训练数据有关。

训练数据中正负样本的比例经常失衡，有大量的负样本和少量的正样本。训练过程中，会导致模型自然预测多数累的概率高于少数类的概率。从而导致过度补偿，对多数类的数据给与了太多的注意，同时对于少数类的注意不够。

简言之，倾斜的数据集会加剧分类器的弱点。导致模型分布于真实分布存在偏差。

1.3 情况分析

我们的目的，是希望模型输出的概率可以看成置信度。但是不同的分类模型，返回的概率存在不同。

逻辑回归(LogisticsRegression) ，默认情况下返回良好的校准概率。因为它直接优化了log-loss情况。
GaussianNB,往往将将概率推到0或1。这样会导致输出的概率过高或过低，与实际不符合。
随机森林分类器等也存在输出概率不能作为置信度的情况。模型中有噪声偏差等因素。

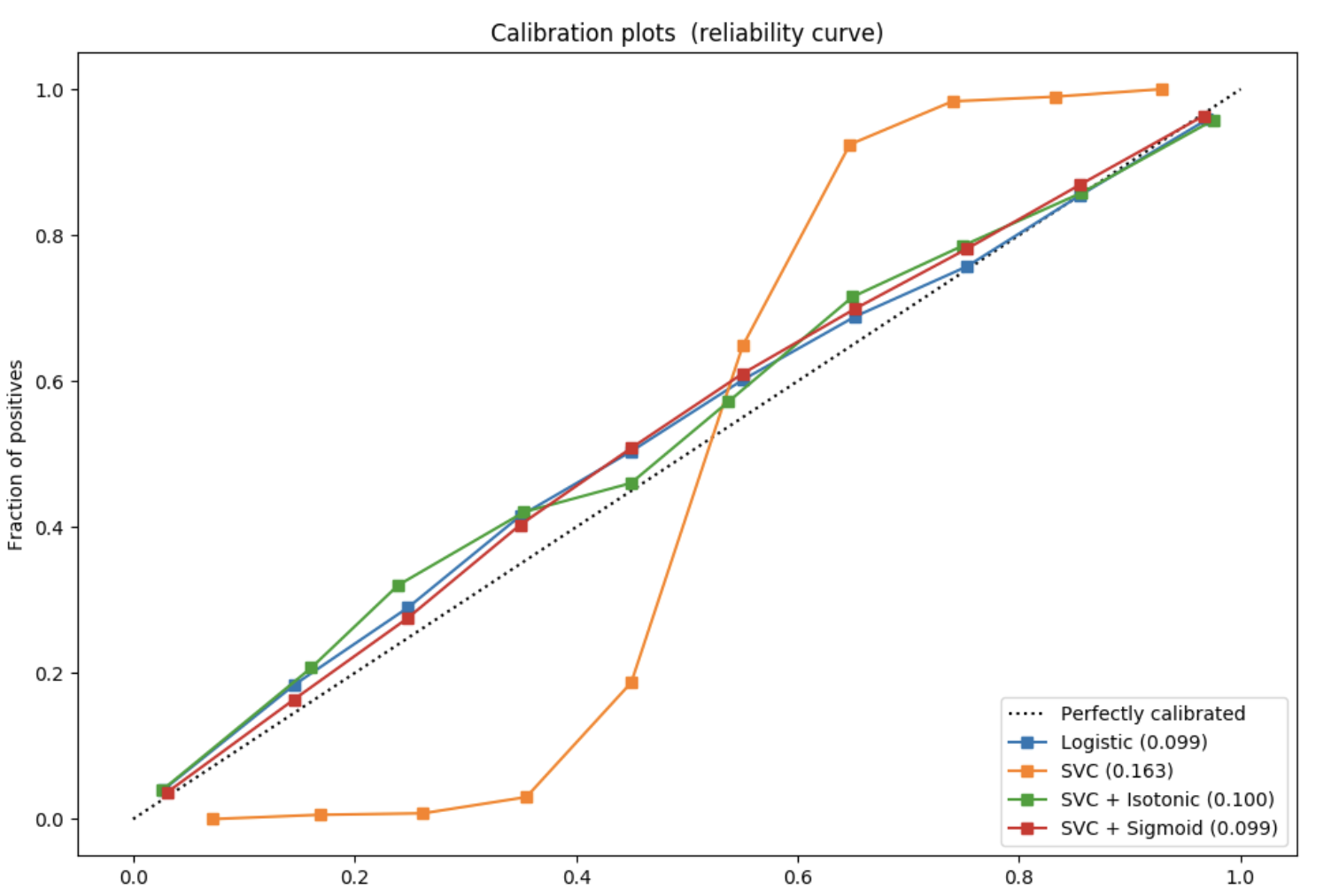
step 1. 横坐标：将预测概率升序排列，选定一个阈值，此时[0，阈值]作为一个箱子。
step 2. 纵坐标：计算这个箱子内的命中率（hit rate），也就是正样本率。
step 3. 选定多个阈值，重复计算得到多个点，连接成线。

可以通过这个图观察模型是否需要进行概率校准。

图中的每个点的坐标为(阈值,命中率)。理想情况下，阈值与命中率应该是一样的。

例如，阈值选择为0.8，计算这个箱子命中率，也就是违约率。如果模型没有错误，那这个违约率应该也近似等于0.8。所以整个图像应该是一条对角线。

标准算法曲线比较像对角线。

缺乏自信的曲线是sigmoid形的，比如SVC，输出概率总在0.5附近。

过于自信的曲线是反sigmoid形的，比如naive bayes，输出概率不是0就是1。

1.4 目的

概率校准的主要目的：

ensure that the scores provided by different scorecards have the same meaning.
确保不同评分卡给出的分数具有相同的含义。
determine or refine the probability estimates to be associated with each score, converted into the actual rate of the outcome (default)
保证预测概率与真实概率之间的一致性（拟合度）。
modifying for the difference between the expected rate based on the historical database and the actual rate observed.
修正实际概率和开发样本中期望概率之间的偏差。

2. 方法

2.1 platt scaling

使用sigmoid函数继续校准，适用于样本量较少的情形，比如风控情况。

step 1. 利用样本特征X和目标变量y训练一个分类器model1。（不限定分类器类型）
step 2. 利用model1对样本预测，得到预测结果out。
step 3. 将预测结果out作为新的特征X'，再利用样本的标签y(真实标签)，训练一个LR。
step 4. LR最后输出的概率值就是platt's scaling后的预测概率。

2.2 保序回归

通常用于数据集较多的情况下。

2.2.1 保序回归介绍

定义：给定一个有限的实数合集 $Y=y_1,y_2,...,y_n$ 以及 $X = x_1,x_2,...,x_n$ ，训练一个模型最小化下列方程。

f(x) = \sum_{i=1}^{n} w_i(y_i-x_i)^2

其中， $x_1<x_2<x_3,...<x_n$

2.2.2 校准流程

step 1. 利用样本特征X和目标变量y训练一个分类器model1。（不限定分类器类型）
step 2. 利用model1对样本预测，得到预测结果f(x),f(x)作为x坐标，将其对应的标签y作为纵坐标构建新的数据集。
step 3. 对(f(x),y)根据f(x)进行排序，排序后作为数据做保序回归。对模型的原始输出做修正

2.3 对比

1. calibration set越大，校准效果越好；
1. Isotonic Regression在calibration set较小时效果要差于Platt Calibration；
1. 在calibration set足够大时，推荐使用Isotonic Regression，因为无需训练而且效果要优于Platt Calibration。

3. 评估

如何定量评估模型校准的好坏

对数损失函数

Log\_Loss = -\sum(y_i*log(p_i)+(1-y_i)*log(1-p_i))

Brier分数

Brier\_Score = \frac{1}{N}\sum_{i=1}^{N}(y_i-p_i)^{2}

其中y表示实际类比，p表示模型估计概率。

两个指标实际上都反映了样本上真实标签与预测概率之间的差异。

4. 代码使用

参考资料：https://www.kesci.com/mw/project/5e7a220b98d4a8002d2cded6/content

基本调库

from sklearn.isotonic import IsotonicRegression
from sklearn.calibration import calibration_curve, CalibratedClassifierCV

Max Blog